
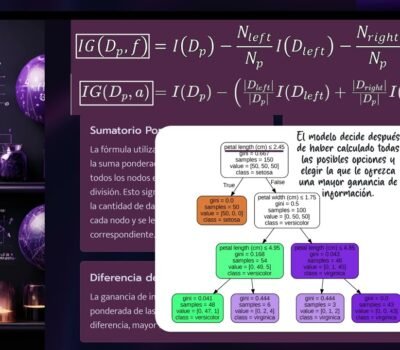
- Introducción al Problema No Lineal y SVM
- Entrenamiento del Modelo SVM en Espacio de Alta Dimensión
- Aplicación de la Función de Mapeo y Clasificación
- Uso de Kernels para Reducir Costos Computacionales
- Ejemplo Práctico con Kernel RBF
- Implementación y Ajustes en SVM con Kernel RBF
- Conclusión y Reflexión Final
Introducción al Problema No Lineal y SVM
En el video anterior, discutimos cómo resolver un problema no lineal utilizando una máquina de soporte vectorial (SVM). El primer paso es transformar los datos de entrenamiento a un espacio de características de mayor dimensión mediante una función de mapeo, denotada con la letra griega fi (φ).
Entrenamiento del Modelo SVM en Espacio de Alta Dimensión
Una vez transformado el espacio de características, procedemos a entrenar un modelo SVM lineal en este nuevo espacio. Gracias a la mayor dimensión, las características se vuelven linealmente separables, lo que nos permite realizar la clasificación mediante un modelo SVM lineal.
Aplicación de la Función de Mapeo y Clasificación
Tras el entrenamiento, empleamos nuevamente la función de mapeo fi (φ) para proyectar los datos de vuelta al espacio de características original, pero esta vez linealmente separables, permitiendo así la clasificación no lineal en esta dimensión.
Uso de Kernels para Reducir Costos Computacionales
A pesar de que aumentar dimensiones suele ser computacionalmente costoso, podemos evitarlo usando funciones kernel. Este método, conocido como el "truco del kernel", logra los mismos resultados pero con un costo reducido. No profundizaremos en la formulación, pero en la práctica simplifica mucho el proceso, como en la transformación de un espacio bidimensional a uno tridimensional sin calcular explícitamente todos los pasos intermedios.
Ejemplo Práctico con Kernel RBF
Uno de los kernels más utilizados es el kernel de función de base radial (RBF), especialmente efectivo en escenarios donde la separación lineal en el espacio original no es posible. El ajuste del parámetro Gamma en este kernel es crucial ya que determina la suavidad de la frontera de decisión. Un valor alto de Gamma resulta en una frontera más ajustada, mientras que un valor bajo la suaviza.
Implementación y Ajustes en SVM con Kernel RBF
Tomamos como ejemplo la clasificación de datos del dataset Iris, un escenario multiclase, para mostrar cómo el ajuste de Gamma afecta los resultados y cómo un valor inadecuado puede llevar a sobreajuste o clasificaciones menos precisas.
Conclusión y Reflexión Final
Al final del video, discuto la importancia del aprendizaje profundo y especializado en temas como estos, que aunque no sean de interés masivo, tienen un impacto significativo en campos especializados. También comparo brevemente con otros intereses más populares, como el fútbol, resaltando la importancia de cada área de conocimiento en diferentes contextos.
Es crucial continuar explorando y adaptando los parámetros de las técnicas de SVM y kernels en diferentes contextos para optimizar el rendimiento y entender las consecuencias prácticas de las decisiones computacionales y teóricas en el proceso de modelado y clasificación.
============================================
Si quieres conocer otros artículos parecidos a ¿Cómo Transforma el Kernel RBF la Ciencia de Datos para ML? Descubre su Poder en la Búsqueda del Hiperplano de Separación. puedes visitar la categoría Jesús Conde.






Deja una respuesta